ABBA
Hadamard style update for LoRA
Overview
We introduce ABBA, a new PEFT architecture that reparameterizes the update as a Hadamard product of two independently learnable low-rank matrices. In contrast to prior work, ABBA fully decouples the update from the pre-trained weights, enabling both components to be optimized freely. This leads to significantly higher expressivity under the same parameter budget. We formally analyze ABBA’s expressive capacity and validate its advantages through matrix reconstruction experiments. Empirically, ABBA achieves state-of-the-art results on arithmetic and commonsense reasoning benchmarks, consistently outperforming existing PEFT methods by a significant margin across multiple models.
Methods
Full fine-tuning and other LoRA methods
Full fine-tuning: Given a pre-trained weight matrix $W_0 \in \mathbb{R}^{m \times n}$, full FT updates all parameters via $W = W_0 + \Delta W$, introducing $m \times n$ trainable parameters per layer. This quickly becomes impractical due to the high memory and compute overhead.
LoRA
HiRA (Hadamard High-Rank Adaptation)
(By the way, the Hadamard product is surprisingly interesting — not as trivial as I initially thought. I wrote a bit more about it here if you’re curious about some of the side paths I explored while working on this idea.)
ABBA
We asked a natural question: what if we no longer kept $W_0$ frozen? What if we made it fully trainable? Unfortunately, this brings us right back to the original challenge of full fine-tuning 😞 — expensive and inefficient. So instead, we apply the classic LoRA trick: decompose the second “frozen” adaptor into a low-rank form and make that trainable. This gives rise to the following update:
\begin{equation} \Delta W = s(B_1 A_1) \odot (B_2 A_2), \end{equation} where $B_1 \in \mathbb{R}^{m \times r_1},\; A_1 \in \mathbb{R}^{r_1 \times n}$ and $B_2 \in \mathbb{R}^{m \times r_2},\; A_2 \in \mathbb{R}^{r_2 \times n}$, with $r_1, r_2 \ll \min(m, n)$ and $s$ is a scaling factor for stability.
# of Parameters $= (r_1 + r_2)(m+n)$
Rank we can express $\le r_1 r_2$ (using Thm (1) again 👀)
Thus, setting $r_1=r_2 = \frac{r}{2}$ not only do we reach the same parameter budget as our baselines but also can represent matrices till rank $\frac{r^2}{4}$ (i.e maximizing the rank max)
Practical stuff while implementing ABBA
Implementing ABBA efficiently
At first glance, applying the Hadamard product directly to two LoRA-style updates — like computing \((B_1 A_1) \odot (B_2 A_2)\) — seems like a nightmare: you’d have to materialize full \(m \times n\) matrices, which is as costly as full fine-tuning. That’s clearly not scalable.
But Theorem 2 gives us a lifeline.
It tells us that instead of computing the big matrices first and then applying the Hadamard product, we can rewrite the whole thing using a row-wise Khatri–Rao product.
This looks and feels just like the standard LoRA decomposition — a skinny-bottleneck sandwich — but with slightly different ingredients. Now we never have to form the full \(m \times n\) matrices explicitly. Instead, we can compute the update as:
\[\Delta W x = B_{\text{kr}} (A_{\text{kr}} x), \quad \text{where } X_{\text{kr}} = X_1 \odot_r X_2 \in \mathbb{R}^{m \times r_1r_2}\]So we preserve the low-rank efficiency, avoid full matrix computation, and still allow more expressive structure than standard LoRA and HiRA.
Note: the representational space isn’t exactly the same as LoRA — see the next section — but the re-parameterization looks very similar to LoRA.
ABBA space is not the LoRA space
A natural question to ask after seeing Theorem 2 is: why not just apply an SVD-style or LoRA-style decomposition directly on the full Hadamard product and solve for matrices $ A_{\text{kr}} $ and $ B_{\text{kr}} $?
In theory, yes — you could compute $ A_{\text{kr}} $ and $B_{\text{kr}}$ as if it were just another low-rank matrix approximation. But here’s the catch: you’d only recover the combined structure (i.e., the matrices $B_{\text{kr}}$ and $A_{\text{kr}}$), and there’s no guarantee that this can be cleanly split back into the original four matrices $ A_1, B_1, A_2, B_2 $. And this is easy to see since each row of the matrix $(B_1 \odot_r B_2)$ belongs to the Segre Variety $\mathcal{S}_{r_1r_2}$ - which is just a fancy way of saying that the space is consists of rank 1 tensors. Think about it $[3,4,6,8] = [1,2] \odot_r [3,4]$ but $[3,4,6,9]$ can’t be represented of the form $u \odot_r v$.
ABBA performs better than SVD
Here we look at the reconstruction error $\vert\vert M - M_X \vert\vert_F^2$ where $M$ is the target matrix and $M_X$ is the matrix of type $X$ where $X = {ABBA, SVD }$.
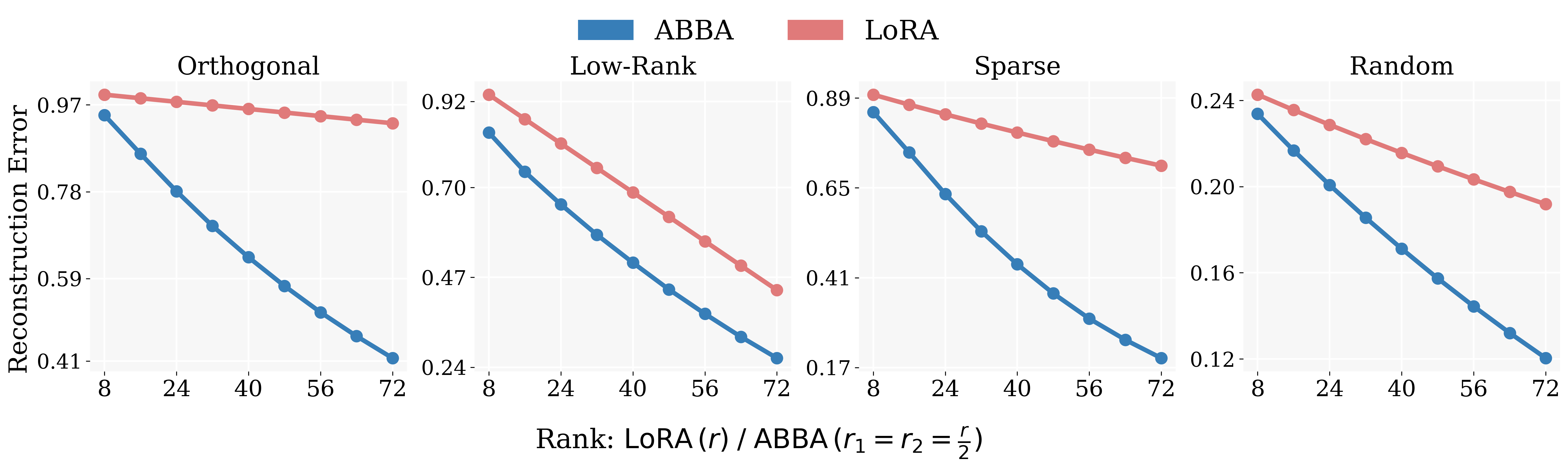
Experiments
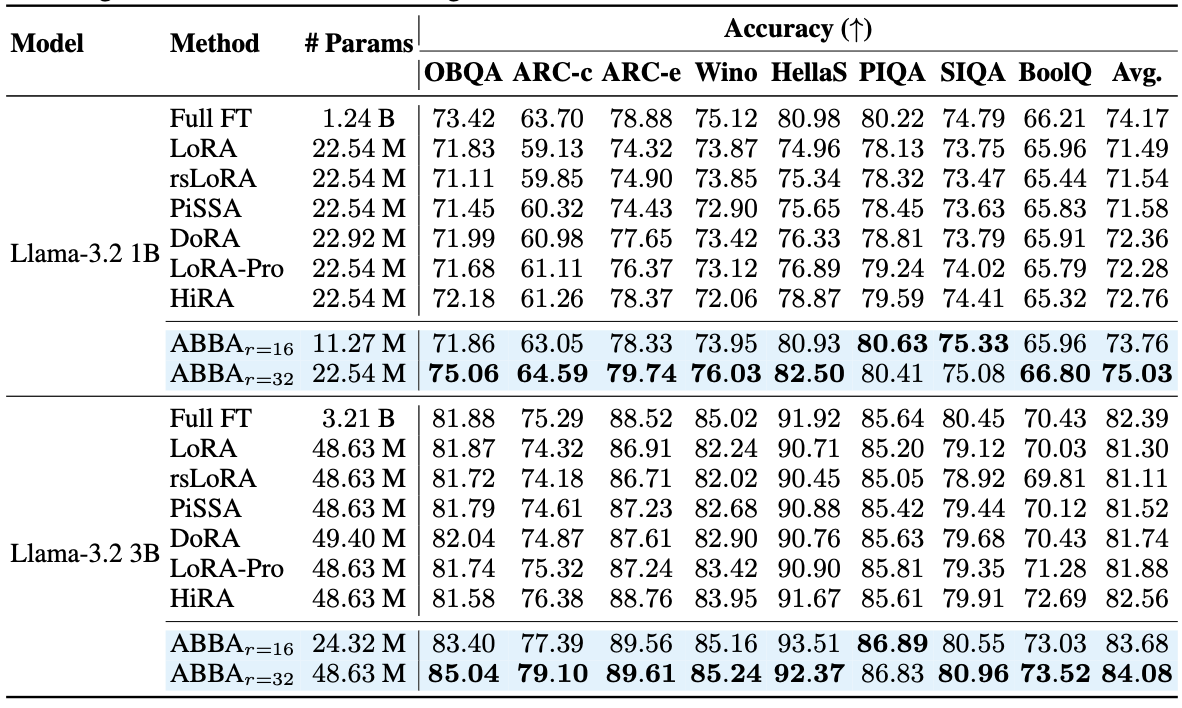
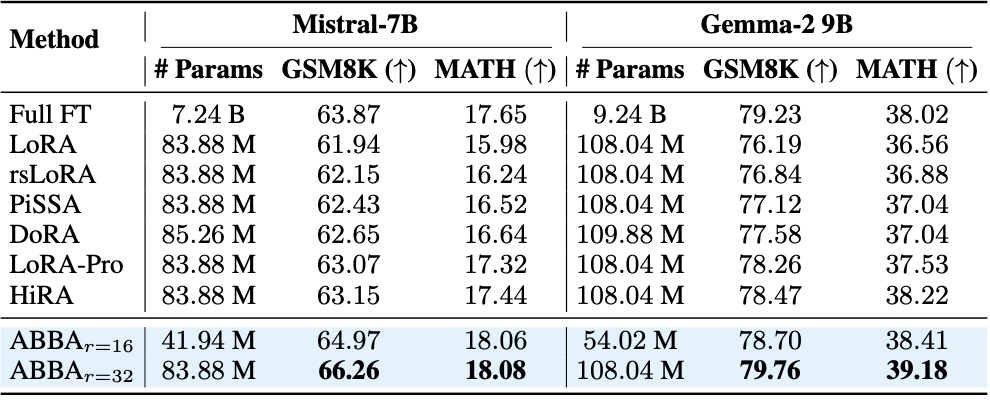
So how does ABBA do experimentally? – it outperforms baselines across Commonsense reasoning and arithmetic reasoning.
Commonsense reasoning
Arithmetic reasoning
Conclusion
ABBA is a simple yet powerful tweak to the PEFT toolkit. By using a Hadamard product of two low-rank matrices, it keeps things lightweight like LoRA but packs in much more expressivity. Across tasks and models, this extra flexibility leads to solid performance gains — all while staying efficient.
We haven’t tested ABBA on vision models or large multimodal setups yet, though it should work there too. Serving many ABBA adapters at once might be a bit heavier due to the Hadamard structure. Also, we don’t explore merging multiple adapters — something that’s known to be tricky in LoRA as well.